VPM For Dummies

The Varying Permeability Model (VPM) for Dummies
By Kevin Watts

  Blog editorial:  I reproduced this article, for wider dissemination, from it’s original location at RebreatherWorld forum

This article attempts to provide a basic framework for looking at the VPM. My hope is that a diver who may be intimidated or frustrated by a mathematical or theoretical presentation of the VPM will get a better working understanding of this important decompression method.

I have employed a building blocks approach to discussing the VPM. Since many reading this article already have a good understanding of the ideas surrounding tissue compartments and dissolved inert gases, I use Buhlmann’s model as a springboard for discussion. Nothing in this article should be read to imply that the VPM was derived from, or is simply a modification of, Buhlmann’s model. The supersaturation limits derived by the VPM completely replace Buhlmann’s M-values as is discussed below. However, there are commonalities between the models and since many readers will bring an understanding of Buhlmann’s model with them, it seemed best to me to start there.

This discussion of the VPM is organized into the following sections:

• Buhlmann’s Dissolved Gas Tissue Model
• VPM Tissue Compartment Modifications
• VPM Bubble Properties
• The No-Bubble-Growth Equation
• Crushing Bubbles
• M-values and vpM-Values
• The Critical Volume Algorithm
• Boyles Law Adjustment (VPM-B)
• A Word About VPM-B/E
• Summary

That’s a tall order so let’s get going. What does the VPM do?

Buhlmann’s Dissolved Gas Tissue Model

The VPM uses the same dissolved gas tissue model used in Buhlmann’s ZH-L16 decompression model. Buhlmann’s model uses 16 hypothetical tissue compartments to simulate the pressures ofdissolved inert gases being absorbed by the body during a dive (on-gassing) and expelled from the body during ascent and following the dive (off-gassing). The 16 compartments on-gas and off-gas at different rates reflecting the fact that not all tissues in your body respond to changes in inspired gas pressure at the same rate. Therefore, the tissue compartment dissolved gas pressure (PTC) will differ among the 16 compartments.

The pressure of dissolved inert gases in your tissues is sometimes referred to as “tissue tension”. In other words, if the inert gas pressure in a tissue compartment is 24.8fsw, then you could also say that the tissue tension is 24.8fsw. As we discuss the VPM I’ll use the term “tissue tension” when speaking of pressures of dissolved gases and “pressure” when speaking of pressures of gases inside bubbles.

VPM Tissue Compartment Modifications 

Buhlmann’s tissue model deals exclusively with dissolved gases. VPM enhances that tissue model by adding a bubble to each tissue compartment. One bubble? Yes, toss one bubble into each of Buhlmann’s 16 tissue compartments.

Now we have 16 compartments tracking dissolved inert gases and one bubble in each of those compartments. Our model now has dissolved gases and free gases (bubbles) interacting! So, as we start our dive Dr. Buhlmann is busily tracking dissolved gases, but we also now have Professor Yount (VPM developer) keeping track of the bubble he just placed in each of our tissue compartments.

Less importantly, the VPM adds carbon dioxide (CO2), water vapor (H2O), and oxygen (O2) into the tissue compartments as well. These gases are modeled as one simple constant (the “Pressure Other Gasses” parameter you see in V-Planner) so computationally it’s a rather simple addition. But because these gases can add to free gases inside the bubble they are reflected by the VPM.

VPM Bubble Properties 

The bubble that Professor Yount just placed in each tissue compartment has specific properties. First, as we begin our dive the Yount bubble is assumed to have a specific size indicated by its radius.

Second, the bubble is permeable, meaning dissolved gases from the tissue compartment can move across the bubble’s “skin” and into the bubble (becoming free gas). If enough pressure is applied to the bubble (such as during a deep descent), the bubble becomes impermeable. At the point of impermeability, further crushing of the bubble becomes more difficult. In any case, you now know how the model got its name – the permeability of the bubble varies.

Third, the bubble has a “skin”, the interface between the free gases inside the bubble and the liquids/dissolved gases in the tissue compartment. The skin possesses specific properties derived from all that bubble experimentation performed by Professor Yount.

Fourth, the bubble is elastic and has a memory. By this I mean that even if a bubble is reduced in size upon descent, and even if the diver remains at that depth indefinitely, the bubble will rebound back to its original size over time (i.e. it “remembers” its original size and moves towards that size over time). This property is not generally important unless you’re a saturation diver because the time it takes to rebound is on the order of weeks. But because you’ll see a parameter in V-Planner related to this property (“Regeneration time constant”), I mention it here.

Finally, and very importantly, the gas pressure inside the bubble (Pb) is known by the following formula:

Pb = Pa + S / r

This equation tells us that the pressure of the gases inside the bubble (Pb) is greater than ambient pressure (Pa) by an amount related to the radius of the bubble (r) and the properties of the bubble’s skin (constant S).

One important thing this formula tells us is that bubbles tend to collapse. Why? Well, if the bubble pressure (Pb) exceeds the pressure outside the bubble (Pa) and the skin is permeable, then gas tends to be driven out of the bubble thereby collapsing it. That’s good.

However, permeability is a double-edged sword. Remember, Professor Yount placed one bubble inside each tissue compartment. That means the bubble is surrounded by liquid holding various levels of dissolved gases. The dissolved gases in each tissue compartment will move across the bubble’s skin into the Yount bubble (thereby inflating the bubble) whenever the compartment’s tissue tension (PTC) exceeds bubble pressure (Pb). This idea is critical and links Buhlmann’s tissue compartment model to Yount’s VPM.

VPM Bubble Property Summary

The No-Bubble-Growth Equation

We are now ready to specify the “no-bubble-growth equation.” Combining the known pressure inside the bubble (Pb) with the knowledge that dissolved gases move into the bubble whenever PTC > Pb, the no-bubble-growth criterion can be stated as follows:

PTC < Pb = Pa + S / r

Now, what does this formula tell us? First, as we’ve already stated, it tells us that the Yount bubble won’t grow if the dissolved gas tension in a compartment is not allowed to exceed the pressure inside the bubble (PTC < Pb).

Second, it tells us that the “appropriate” tissue tension during ascent is related to ambient pressure (Pa), the size of the bubble (r) and the bubble’s skin (S).

Third, it tells us that larger bubbles require the diver to maintain lower dissolved gas tensions. Why? Larger bubbles (increasing r) decrease the S/r term. Intuitively this must seem obvious – development of larger bubbles must require more conservative decompression.

Finally, consider a simple rewrite of the no-bubble-growth equation:

PTC – Pa < S / r

This equation is obtained by subtracting ambient pressure (Pa) from both sides of the equation. The term PTC – Pa defines a tissue compartment’s “supersaturation”. Supersaturation is just a way of saying that the dissolved gas tension in a compartment exceeds ambient pressure. This form of the no-bubble-growth equation tells us that the supersaturation level allowed by the VPM is a simple function of the size of the bubble. As you can imagine, then, an important task of the VPM is determining the size (radius) of the Yount bubble.

Crushing Bubbles

As we have seen, the Yount bubble size is a key player in the VPM. Keeping track of the size reduction in the Yount bubble during the crushing pressures encountered during a diver’s descent is a critical task of the VPM.

It’s important to realize that the crushing pressure is not based on the maximum ambient pressure (depth) experienced by the diver. Rather, the amount by which the size of the Yount bubble shrinks is a function of the difference between ambient pressure and the dissolved gas tension in the tissue compartment (Pa – PTC).

Using Pa – PTC as the primary crushing mechanism has a couple of implications. First, since the tissue tension may vary considerably between compartments, the size of the Yount bubble in each compartment is reduced by different amounts. The bubble in faster compartments is reduced less, sometimes considerable less, than slower compartments. Why? Because faster compartments adjust to ambient pressure more quickly thereby minimizing Pa – PTC. Second, immediate fast descents to the maximum dive depth require less decompression than slower descents. Again, the faster you descend the less time the tissue tension in the faster compartments has to adjust to ambient pressure (i.e. you maximize Pa – PTC).

This behavior provides a possible explanation for why decompression for reverse profiles should be handled more conservatively. A dive that stops initially at 150fsw and then descends further to 300fsw produces less bubble-reducing-crushing-pressure than a dive with an immediate descent to 300fsw. By immediately descending to 300fsw, the diver doesn’t allow the faster compartments to “catch-up” to ambient pressure.

Importantly, the crushing of the bubble in each compartment is not reversed simply by ascending. In other words, the bubble is reduced in size (crushed) on descent, but unless tissue tensions are allowed to exceed the no-bubble-growth tension during ascent, the Yount bubble is not assumed to grow. An exception to this occurs when applying the Boyles Law Adjustment (VPM-B) after entering the decompression zone, but we’ll discuss that topic later.

One might ask why a diver doesn’t simply descend as far as possible since that will achieve maximum reduction in bubble size and, therefore, will increase the allowed tissue tension during ascent. There are two responses. First, you must keep focused on the dissolved inert gases loaded due to additional depth. Professor Yount may very well be happy about the further reduction in his bubble’s size, but Dr. Buhlmann will be right there lecturing you about the additional inert gases being absorbed by his tissue compartments. Second, remember that the bubble becomes impermeable once the crushing pressure exceeds the “Gradient onset of impermeability” parameter. This shift to impermeability further slows reductions in bubble size.

M-Values and vpM-Values

At this point you may already see the basic VPM ascent strategy forming. Very simply, the VPM algorithm is this:

1. Let Buhlmann track dissolved gases and Yount track bubble radius, especially the crushing of the bubble during descent.
2. At each point in the ascent, calculate bubble pressure (Pb).
3. Since the Yount bubbles only grow when the compartment’s tissue tension (PTC) exceeds bubble pressure (Pb), stop the diver whenever a compartment’s tissue tension is about to exceed the compartment’s bubble pressure (Pb).

That’s it!

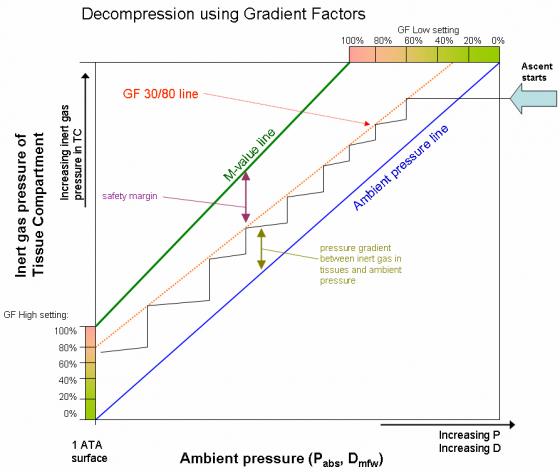
Now, some of you may be thinking, “Hey, wait a minute. This looks familiar!” You’re right. This idea of limiting tissue tension as a way of staging ascents is not new. In fact it’s the same ascent strategy used by Buhlmann’s M-values and Erik Baker’s Gradient Factors.

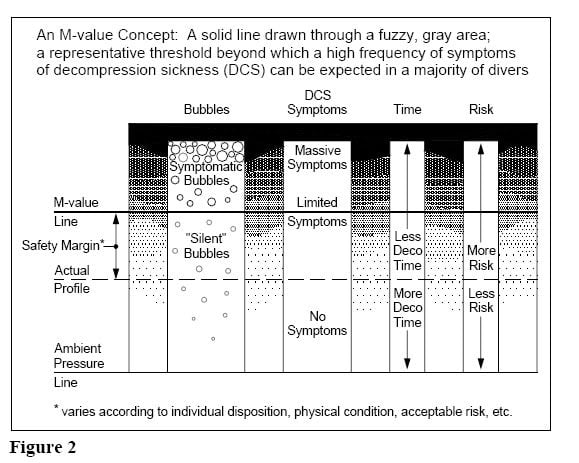
One way to look at “M-Values” is that they are simply maximum supersaturation tensions allowed by a decompression model. Buhlmann’s M-values define each tissue compartment’s allowable tension at a given depth via a linear equation. The M-value generated by that equation tells you when Buhlmann thinks the tissue tension for that compartment at that depth is too high. Buhlmann’s M-values were derived empirically (i.e. by looking at dives to see who got bent).

The VPM also stages divers by limiting tissue tensions during ascent. In this sense, the VPM produces its own “vpM-Values”. But, rather than being derived empirically, these vpM-values are determined by the no-bubble-growth equation. The no-bubble-growth equation is dependent on the specific characteristics of your dive, the parameters of VPM, and their combined effect on the Yount bubble. But, it is important to understand that the VPM still stages divers by limiting dissolved gas tensions, the same basic staging paradigm used by Buhlmann.

Now, just based on what we’ve discussed to this point, let’s take a look at a relatively benign dive profile – 20 min @ 100ft on air. Let’s see how these Yount bubbles generate a profile.

The table below shows profiles for VPM (using only the no-bubble-growth equation), RGBM (nominal), and GF 30/85.

20 min @ 100ft Air – All values are total runtime

The VPM-no-bubble-growth model produces a 30 minute ascent for a 20 minute dive to 100ft. This is not a very compelling result and indicates more work is ahead.

The Critical Volume Algorithm

Simply relying on the no-bubble-growth equation to produce profiles is too conservative to be useful in many cases, especially near the no decompression limit. So, what if we relaxed the “no-bubble-growth” criterion and adopted a “not-too-much-bubble-growth” criterion? That thought is developed in the Critical Volume Algorithm (CVA).

The CVA intentionally allows the diver to exceed the tissue tensions indicated by the no-bubble-growth equation. Exceeding the no-bubble-growth tensions means the Yount bubbles placed in our tissue compartments will start growing. What the CVA hypothesizes is that our bodies must deal pretty well with a certain volume of free gases, but over that “critical volume” we start seeing symptoms of DCS. The task, then, is to develop some approach to approximating when too much gas is accumulating in bubbles.

The VPM estimates excess bubble volume by estimating the amount by which a diver exceeds the no-bubble-growth tissue tension (excess tension) and the time the diver is exposed to that excess tension. You can explore the development of the CVA elsewhere. However, just realize that the CVA is a mix of theory and empirical tuning. The theory helped develop a reasonable formula that one might expect to produce higher values when underlying conditions might permit more bubble growth and lower values when conditions might produce less bubble growth. The empirical tuning is the dialing-in of the theoretical formula to real world decompression data. The “Critical Volume Lambda” parameter you see in V-Planner represents the “tuning” of the CVA formula.

Here’s how the CVA works. First, V-Planner or your dive computer runs a VPM profile based on no-bubble-growth. Then, the computer relaxes the no-bubble-growth tissue tension and produces another profile. The new profile may cause the critical volume to be exceeded. In that case, the computer runs another profile with tissue tensions tightened-up a bit. This process continues until the CVA hits its critical volume target. The CVA’s back-and-forth search for the critical volume is the reason the VPM is described as an “iterative algorithm”.

Now, how does the VPM-CVA profile look for our 20 min air dive to 100fsw.

20 min @ 100ft Air – All values are total runtime

Much better! The CVA has done its job and produced a profile much more in line with reasonable expectations. The CVA is an integral part of the VPM. From now on, when we speak of the VPM we’ll assume the CVA is operating.

Boyles Law Adjustment (VPM-B)

Now consider another profile. The table below was generated for a 25 min dive to 325ft using Tx10/50 with switches to EAN50 at 70ft and O2 at 20ft.

25 min @ 325ft Tx10/50 Switch EAN50 @ 70ft and O2 @ 20ft
All values are total runtime

This VPM profile surfaces 31 minutes sooner than RGBM and 80 minutes sooner than GF 30/85. It would appear that these more extreme dives also require some adjustment.

One place the VPM looked for guidance was Boyle’s Law. Boyle’s law should be very familiar to divers. The “-B” adjustment uses Boyle’s law to increase the bubble radius during ascent. At this point you should immediately be thinking, “Increased bubble radius means more conservative profile.”

The Boyle’s law adjustment accomplishes the following:

1. it introduces a gas expansion component into the VPM algorithm,
2. it provides a systematic, scientific-type adjustment rather than an ad-hoc adjustment,
3. it adds conservatism to the profile (but you already knew that).

As with other parts of the VPM, incorporating a Boyle’s gas expansion adjustment into the VPM is part theory, part reflection of empirical data. The newly modified model was renamed VPM-B.

Here’s how the Boyle’s law adjustment works:

1. At the first decompression stop, the VPM notes the size of each compartment’s bubble.
2. At each succeeding stop, it increases the radius of each Yount bubble by the amount predicted by Boyle’s law due to the drop in ambient pressure.
3. The allowable tissue tension at each succeeding stop is reduced due to the larger bubble radius. Therefore, the diver must stay longer at that stop to wait for his tissue tension to drop to this new lower tension limit.

The impact of the Boyle’s Law Adjustment to the previous profile is shown below.

25 min @ 325ft Tx10/50 Switch EAN50 at 70ft and O2 at 20ft
All values are total runtime

Our VPM-B profile is now 42 minutes longer. The impact of the Boyles Law Adjustment on many dive profiles is not nearly so extreme, but decompression for deeper, longer dives is materially lengthened.

A Word About VPM-B/E

The VPM algorithm made public by Eric Baker is implemented in V-Planner, a popular dive planning tool. V-Planner has also implemented an extension to the VPM called “VPM-B/E”.

The /E extension, not really contemplated by the VPM, is meant to add conservatism for more extreme dives when a diver believes it is prudent to add more conservatism to the VPM-B profile. Of course, one challenge in implementing an extension is determining when a certain profile requires “padding”.

Unfortunately, the /E extension is proprietary and no real information about its inner workings is publicly available. However, I’ve had good results mirroring the /E extension by increasing the Yount bubble size in the shallow stops (< 70fsw) in rough proportion to the amount by which VPM-B violates Buhlmann’s surfacing M-Value.

The technique used to roughly mirror the extension is relatively straightforward to implement as only minor modifications to Eric Bakers’s code are required. However, since the /E extension is proprietary, the actual technique used may be quite different than that described above, but with similar effect.

Summary

The Varying Permeability Model can be thought of as a layered decompression model. The base layer of the model deals with the Yount bubble and the no-bubble-growth tissue tensions that keep the Yount bubble from initiating growth.

The Critical Volume Algorithm is layered on top of this base layer in order to produce profiles that seamlessly intercept known no-decompression-limits. The CVA’s largest impact is near the NDLs and has limited impact on more extreme dives.

The next layer incorporates Boyle’s Law Adjustment. This adjustment has a large impact on more extreme dives and more limited impact as the diver moves toward the NDLs. Obviously, both the CVA and the Boyle’s adjustment impact all dives, but their maximum effect occurs at the opposite ends of the dive spectrum.

Finally, the /E extension adds more time onto VPM-B profiles that violate Buhlmann’s surfacing M-Value (apparently). The /E extension is the final layer.

This article barely touches upon the theoretical underpinnings of the VPM. I’ve omitted or only partially represented some key VPM concepts. For example, the Yount bubble represents the dividing line between growing and non-growing bubbles in a theorized distribution of bubbles. Also, if you dive with helium in your mix, two bubbles with different sizes are used in each compartment, not just one.

You get the idea. While I believe the framework for thinking about the VPM presented in this article is sufficiently accurate, it certainly doesn’t paint the entire picture. However, my hope is that in some measure this article provides additional clarity for some divers, and that the simplifications employed to enhance clarity strike an appropriate balance between clarity and truth.

Safe Diving!

DECOMPRESSION DIVING IS INHERENTLY RISKY! This article does not constitute an endorsement, or a critique, of the VPM or any other decompression model. Decompression models are mathematical constructs that can’t possibly reflect the complex changes your body goes through during decompression. Decompression models are, at best, approximations. Following any modern decompression schedule including the VPM, VPM-B, or VPM-B/E does not guarantee you won’t get decompression sickness.