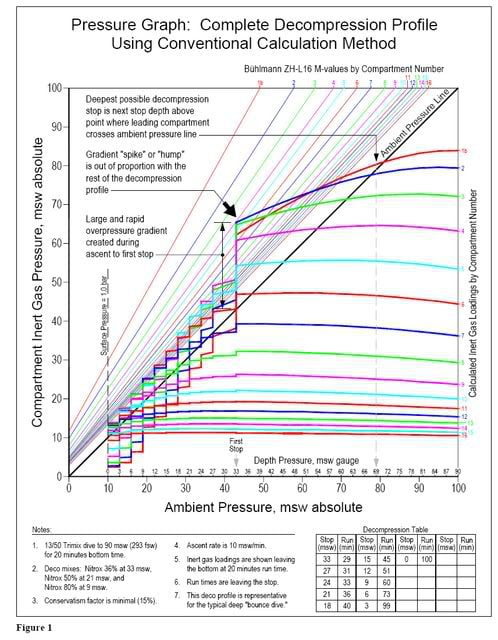
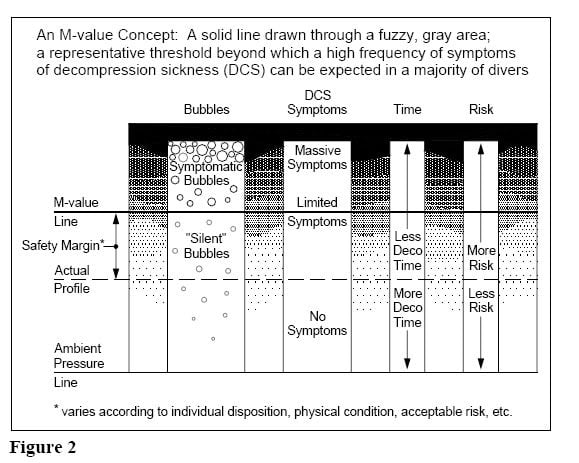
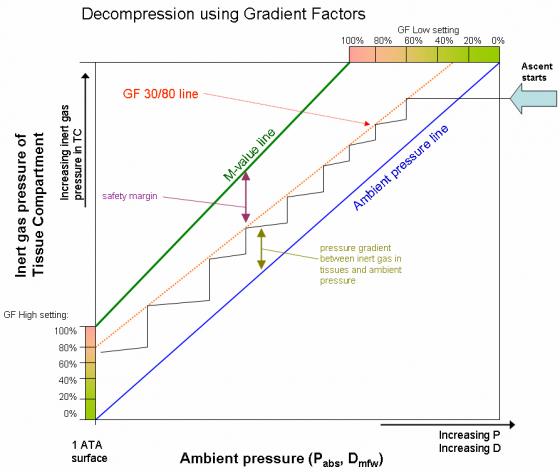
Calculating No Stop Time for Scuba Diving
Welcome to an informative article on “Calculating No Stop Time for Scuba Diving” written by Erik C. Baker. This article is specifically designed for recreational divers who want to learn about the source theory and calculations involved in determining no stop times during their dives.
By reproducing this article on our website, I aim to make this valuable source information easily accessible and available online for everyone.
In this article, you will get to learn about the calculations and formulas developed from the basic Haldane equation. So, keep reading to gain a deeper understanding of the no-stop time calculation for scuba diving.
About Erik Baker
Erik C. Baker is a well-known figure in the world of technical diving, with a focus on decompression models and dive planning. He is an electrical engineer with a consulting engineering firm in Florida who has developed several computer programs to improve the safety of his cave and trimix diving.
Baker’s contributions to the diving community include articles on decompression models, such as his work on understanding M-values and the use of deep stops. He has also developed computer programs for dive planning, including those used to manage exposure to oxygen toxicity. Additionally, he has written about calculating the “No-Stop Time” for divers breathing only one inert gas, such as air or nitrox.
Calculating ‘No Stop Time’ explains how to calculate the amount of time a diver can spend at a given depth without needing to make a decompression stop.
This calculation is based on the Haldane equation, which describes gas loading in tissues during a constant-depth dive. Baker also wrote about the importance of proper decompression planning and avoiding decompression sickness in technical diving.
Calculating ‘No Stop Time’ by Erik C. Baker
The following is an explanation about calculating the “No Stop Time”:
Starting out with the basic Haldane equation (keep in mind that this equation is for a CONSTANT DEPTH profile, not for ascents or descents):
P = Po + (Pi – Po)(1 – e^-kt)
which states that P, the final partial pressure in a given compartment (as a function of time), will be the initial partial pressure, Po, plus (or minus) the exponential gas loading that takes place. The exponential gas loading is given by the second part of the equation, (Pi – Po)(1 – e^-kt).
Note that Pi – Po is the pressure gradient between the inspired gas pressure and the initial compartment pressure. This is the “driving force” for on-gassing and off-gassing.
Re-arranging the Haldane equiation
You can rearrange the Haldane equation to solve for time, t:
(P – Po)/(Pi – Po) = 1 – e^-kt
e^-kt = 1 – (P – Po)/(Pi – Po)
Before you take the natural logarithm of both sides, you should simplify the equation further (you did not do this in your post):
e^-kt = (Pi – Po)/(Pi – Po) – (P – Po)/(Pi – Po)
e^-kt = [(Pi – Po)-(P – Po)]/(Pi – Po)
e^-kt = (Pi – Po – P + Po)/(Pi – Po)
e^-kt = (Pi – P)/(Pi – Po)
Now take the natural logarithm of both sides:
ln[e^-kt] = ln[(Pi – P)/(Pi – Po)]
-kt = ln[(Pi – P)/(Pi – Po)]
t = (-1/k)*ln[(Pi – P)/(Pi – Po)]
This time, t, is the time that it will take for the compartment to load gas (on-gas or off-gas) from the initial compartment pressure, Po, to the final pressure, P.
Substitute the surfacing M-value
You can substitute the surfacing M-value, Mo, for the final pressure, P:
t = (-1/k)*ln[(Pi – Mo)/(Pi – Po)]
In this case, the time, t, is the “No Stop Time” or “No Decompression Limit” (NDL) based on the present gas loading, Po, and the inspired gas pressure, Pi.
An example dive
A diver begins an air dive by descending to a depth of 30 meters of seawater (msw) very rapidly. Let’s assume that it was an “instantaneous” descent. Now he is on the bottom at 30 msw. What is the “No Stop Time” or “No Decompression Limit” for this depth?
Note: Remember all pressures are ABSOLUTE!
Factoring ambient pressure into no stop time
Assuming the dive is from sea level, the ambient pressure is the depth pressure of 30 msw plus the surface barometric pressure of 10 msw:
Pamb = 30 msw + 10 msw = 40 msw
The inspired pressure is the ambient pressure minus the water vapor pressure (Buhlmann value) times the fraction of inert gas:
Pi = (Pamb – PH2O)FN2 = (40 msw – 0.627 msw)0.79 = 31.1 msw
The initial compartment pressure will be due to breathing atmospheric air at the surface for a long time (first dive of the day):
Po = (Pamb – PH20)FN2 = (10 msw – 0.627 msw)0.79 = 7.4 msw
Surfacing M-values vary by compartment
The surfacing M-values will vary by compartment. Example: for Compartment No. 2 using the Buhlmann ZH-L16B M-values, Mo = 25.4 msw.
The time constant, k, for Compartment No. 2 is the natural logarithm of 2 divided by the half-time:
k (Cpt 2) = ln2/half-time = 0.693/8 min = 0.086625
Now we can compute the “No Stop Time” or NDL for this compartment:
t = (-1/k)*ln[(Pi – Mo)/(Pi – Po)]
t (Cpt 2) = (-1.0/0.086625)*ln[(31.1 – 25.4)/(31.1 – 7.4)]
t (Cpt 2) = 16.45 minutes
This process is repeated for each compartment and the shortest time computed across all compartments is the NDL for the profile.
You cannot apply the No Stop Time under this condition
VERY IMPORTANT NOTE: You cannot apply the “No Stop Time” equation: t = (-1/k)*ln[(Pi – Mo)/(Pi – Po)], under the following conditions:
- If the quantity within the logarithm bracket is a negative number. This is because the logarithm of a negative number is a complex number (i.e. a + ib) which is NOT A REAL situation for diving!
The quantity within the logarithm bracket will be negative if:
- Mo > Pi > Po
- Mo < Pi < Po
- If Pi = Po then there will be division by zero which cannot be accomplished.
- If the quantity within the logarithm bracket is a positive number greater than one (1), then the time computed in the overall equation will be negative, which is NOT A REAL situation for diving!
Surfacing M-values in the logarithm
The quantity within the logarithm bracket will be positive and greater than one (1) if:
- Mo < Pi > Po
- Mo > Pi < Po
THEREFORE, the “No Stop Time” equation, t = (-1/k)*ln[(Pi – Mo)/(Pi – Po)], can only be applied when:
- Pi > Mo > Po (on-gassing), or
- Pi < Mo < Po (off-gassing)
In other words, Mo, has to be a value between the present value of Pi and Po.
For the typical sport diving application, the “No Stop Time” equation will be applied only for condition A above, that is when,
Pi > Mo > Po (on-gassing)
The program must include the logic to account for this requirement. An example
of this is as follows:
NOSTOP = 0.0
DO 100 I = 1,16
IF ((PIN2 .GE. MVALUE(I)) .AND. (MVALUE(I) .GT. PN2O(I)) THEN TIME(I) = -1.0/KN2(I)*ALOG((PIN2 – MVALUE(I))/(PIN2 – PN2O(I)))
NOSTOP = MIN(NOSTOP, TIME(I))
END IF
100 CONTINUE
The “No Stop Time” calculation will be applied after each change in depth during the dive (if it is being calculated in real-time). Of course, the dive computer will still need to keep track of the gas loadings separately during the dive as well.
Scuba Diving No Stop Time Summary
Calculating No Stop Time for Scuba Diving refers to the maximum amount of time that a scuba diver can safely spend underwater at a certain depth without requiring a decompression stop. Several factors determine No Stop Time, including the dive’s depth, duration, and breathing gas mixture.
No stop time and NDL
It’s important to note that most recreational dives have a No Decompression Limit (NDL), which is the maximum time a diver can spend at a particular depth without requiring a decompression stop. For instance, the NDL at 60 feet is 55 minutes. If a diver exceeds the NDL, they must make decompression stops to prevent decompression sickness.
Surface interval time
Moreover, scuba divers must also factor in the surface interval time (SIT) between dives, which determines the repetitive dive timetable. A repetitive dive timetable allows divers to make successive dives while avoiding decompression sickness.
NAUI and US Navy diving tables
NAUI Dive Tables are a set of tables based on the US Navy Decompression Tables and are designed explicitly for recreational diving. They consist of three factors:
- End-Of-Dive Letter Group
- Surface Interval Time (SIT) Table
- Repetitive Dive Timetable
DAN recommendations on flying after diving
Finally, DAN recommends allowing a minimum of:
- 24 hours before flying after any dive to account for variables such as fatigue and dehydration
- Single dives within the No Decompression Limits require a minimum of 12 hours before flying
- Repetitive dives of multiple days require at least 18 hours.
- Decompression dives (planned or unplanned) require substantially more time
In summary, calculating No Stop Time for Scuba Diving is critical to ensure divers don’t exceed the No Decompression Limit and make decompression stops. Divers must also consider other factors such as the repetitive dive timetable, surface interval time, and DAN’s recommendations before flying.
About The Author

Andy Davis is a RAID, PADI TecRec, ANDI, BSAC, and SSI-qualified independent technical diving instructor who specializes in teaching sidemount, trimix, and advanced wreck diving courses.
Currently residing in Subic Bay, Philippines; he has amassed more than 10,000 open-circuit and CCR dives over three decades of challenging diving across the globe.
Andy has published numerous diving magazine articles and designed advanced certification courses for several dive training agencies, He regularly tests and reviews new dive gear for scuba equipment manufacturers. Andy is currently writing a series of advanced diving books and creating a range of tech diving clothing and accessories.
Prior to becoming a professional technical diving educator in 2006, Andy was a commissioned officer in the Royal Air Force and has served in Iraq, Afghanistan, Belize, and Cyprus.
In 2023, Andy was named in the “Who’s Who of Sidemount” list by GUE InDepth Magazine.
Purchase my exclusive diving ebooks!
Originally posted 2018-03-07 23:54:23.