In conjunction with an array of hypothetical “tissue” compartments, gas loading calculations and M-values compose the major elements of the dissolved gas or “Haldanian” decompression model.
Through the use of widely-available desktop computer programs, technical divers rely on this model for their decompression safety.
A good understanding of M-values can help divers to determine appropriate conservatism factors and evaluate the adequacy of various decompression profiles for a particular dive.
What are M-Values?
The term “M-value” was coined by Robert D. Workman in the mid-1960’s when he was doing decompression research for the U.S. Navy Experimental Diving Unit (NEDU). Workman was a medical doctor with the rank of Captain in the Medical Corps of the U.S. Navy.
The “M” in M-value stands for “Maximum.“
For a given ambient pressure, an M-value is defined as the maximum value of inert gas pressure (absolute) that a hypothetical “tissue” compartment can “tolerate” without presenting overt symptoms of decompression sickness (DCS).
M-values are representative limits for the tolerated gradient between inert gas pressure and ambient pressure in each compartment. Other terms used for Mvalues are “limits for tolerated overpressure,” “critical tensions,” and “supersaturation limits.”
The term M-value is commonly used by decompression modelers.
HISTORICAL BACKGROUND
In the dissolved gas or “Haldanian” decompression model, gas loading calculations for each hypothetical “tissue” compartment are compared against “ascent limiting criteria” to determine the safe profile for ascent.
John S. Haldane
In the early years of the model, including the method developed by John S. Haldane in 1908, the ascent limiting criteria was in the form of “supersaturation ratios.”
For example, Haldane found that a diver whose “tissues” were saturated by breathing air at a depth of 33 fsw could ascend directly to the surface (sea level) without experiencing symptoms of DCS.
Because the ambient pressure at 33 fsw depth is twice that at sea level, Haldane concluded that a ratio of 2:1 for tolerated overpressure above ambient could be used as the ascent limiting criteria.
Supersaturation Ratio
This approximate ratio was used by Haldane to develop the first decompression tables. In later years, and up until the 1960’s, other ratios were used by various modelers for the different halftime compartments.
Most of the U.S. Navy decompression tables were calculated using this supersaturation ratio method.
However, there was a problem. Many of the tables produced by this method were deficient when it came to deeper and longer dives.
Robert Workman
Robert Workman began a systematic review of the decompression model including previous research that had been performed by the U.S. Navy. He arrived at some important conclusions.
First of all, he recognized that Haldane’s original ratio of 2:1 (based on air) was really a ratio of 1.58:1 if you considered only the partial pressure of the inert gas in air _ nitrogen.
[By that time in decompression research it was known that oxygen was not a significant factor in DCS; it was the inert gases like nitrogen and helium that were the culprits.]
In his review of the research data, Workman found that the “tissue ratios” for tolerated overpressure varied by halftime compartment and by depth.
Maximum Tolerated Partial Pressure
The data showed that the faster halftime compartments tolerated a greater overpressure ratio than the slower compartments, and that for all compartments the tolerated ratios became less with increasing depth.
Then, instead of using ratios, Workman described the maximum tolerated partial pressure of nitrogen and helium for each compartment at each depth as the “M-value.”
Next, he made a “linear projection” of these M-values as a function of depth and found that it was a reasonably close match to the actual data. He made the observation that “a linear projection of Mvalues is useful for computer programming as well.”
Sponsored Link
THE WORKMAN M-VALUES
Workman’s presentation of M-values in the form of a linear equation was a significant step in the evolution of the dissolved gas decompression model.
His M-values established the concept of a linear relationship between depth pressure [or ambient pressure] and the tolerated inert gas pressure in each “tissue” compartment.
This concept is an important element of the present day dissolved gas model as applied by a variety of modelers.
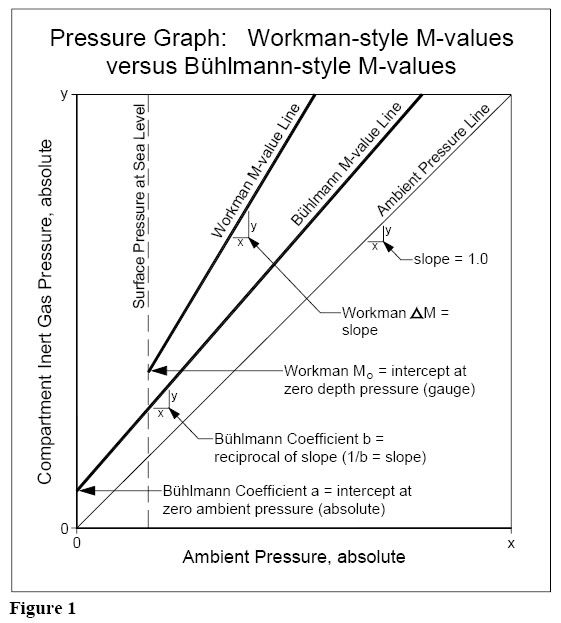
Workman expressed his M-values in the slope-intercept form of a linear equation (see Figure 1). His surfacing value was designated M? [pronounced “M naught”].
This was the intercept value in the linear equation at zero depth pressure (gauge) at sea level. The slope in the linear equation was designated ?M or DM [pronounced “delta M”] and represented the change in M-value with change in depth pressure.
THE BÜHLMANN M-VALUES
Professor Albert A. Bühlmann
Professor Albert A. Bühlmann, M.D., began doing decompression research in 1959 in the Laboratory of Hyperbaric Physiology at the University Hospital in Zürich, Switzerland. Bühlmann continued his research for over thirty years and made a number of important contributions to decompression science.
In 1983 he published the first edition (in German) of a successful book entitled Decompression _ Decompression Sickness. An English translation of the book was published in 1984.
Bühlmann’s book was the first nearly complete reference on making decompression calculations that was widely available to the diving public.
As a result, the “Bühlmann algorithm” became the basis for most of the world’s in-water decompression computers and do-it-yourself desktop computer programs.
Three more editions of the book were published in German in 1990, 1993, and 1995 under the name Tauchmedizin or “Diving Medicine.” [An English translation of the 4th Edition of the book (1995) is in preparation for publication].
Bühlmann’s method for decompression calculations was similar to the one that Workman had prescribed. This included M-values which expressed a linear relationship between ambient pressure and tolerated inert gas pressure in the hypothetical “tissue” compartments.
The Difference Between Workman and Bühlmann M-Values
The major difference between the two approaches was that Workman’s M-values were based on depth pressure (i.e. diving from sea level) and Bühlmann’s M-values were based on absolute pressure (i.e. for diving at altitude).
This makes sense, of course, since Workman was concerned with the diving activities of the U.S. Navy (presumably performed at sea level) while Bühlmann was concerned with diving activities in the high mountain lakes of Switzerland.
Different Bühlmann Decompression Models
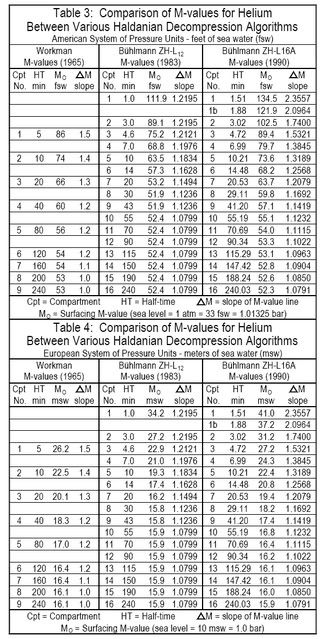
Bühlmann published two sets of M-values which have become well-known in diving circles; the ZH-L12 set from the 1983 book, and the ZH-L16 set(s) from the 1990 book (and its later editions).
The “ZH” in these designations stands for “Zürich” (named after his hometown), the “L” stands for “limits,” and the “12” or “16” represents the number of pairs of coefficients (M-values) for the array of half-time compartments for helium and nitrogen.
The ZH-L12 set has twelve pairs of coefficients for sixteen half-time compartments and these M-values were determined empirically (i.e. with actual decompression trials).
The ZH-L16A set has sixteen pairs of coefficients for sixteen half-time compartments and these M-values were mathematically-derived from the half-times based on the tolerated surplus volumes and solubilities of the inert gases.
The ZH-L16A set of M-values for nitrogen is further divided into subsets B and C because the mathematically-derived set A was found empirically not to be conservative enough in the middle compartments.
The modified set ZH-L16B (slightly more conservative) is suggested for table calculations and the modified set ZH-L16C (somewhat more conservative) is suggested for use with in-water decompression computers which calculate in real-time.
Similar to the Workman M-values, the Bühlmann M-values are expressed in the slope-intercept form of a linear equation (see Figure 1). The Coefficient a is the intercept at zero ambient pressure (absolute) and the Coefficient b is the reciprocal of the slope.
[Note: the Coefficient a does not imply that humans can withstand zero absolute pressure! This is simply a mathematical requirement for the equation. The lower limit for ambient pressure in the application of the Bühlmann M-values is on the order of 0.5 atm/bar.]
DCAP AND DSAT M-VALUES
Many technical divers will recognize the 11F6 set of M-values used by Hamilton Research’s Decompression Computation and Analysis Program (DCAP). This set or “matrix” of M-values was determined by Dr. Bill Hamilton and colleagues during development of new air decompression tables for the Swedish Navy.
In addition to air diving, the 11F6 M-values have worked well for trimix diving and are the basis for many custom decompression tables in use by technical divers.
The PADI RDP
Many sport divers are familiar with the Recreational Dive Planner (RDP) distributed by the Professional Association of Diving Instructors (PADI).
The M-values used for the RDP were developed and tested by Dr. Raymond E. Rogers, Dr. Michael R. Powell, and colleagues with Diving Science and Technology Corp. (DSAT), a corporate affiliate of PADI. The DSAT M-values were empirically verified with extensive in-water diver testing and Doppler monitoring.
Sponsored Link
COMPARISON OF M-VALUES
Tables 1 thru 4 present a comparison of M-values for nitrogen and helium between the various Haldanian decompression algorithms discussed in this article.
All M-values are presented in Workman-style format. An evolution or refinement in the M-values is evident from Workman (1965) to Bühlmann (1990).
The general trend has been to become slightly more conservative.
This trend reflects a more intensive validation process (empirical testing) and includes the use of Doppler ultrasound monitoring for the presence and quantity of “silent bubbles” (bubbles which are detectable in the circulation but are not associated with overt symptoms of decompression sickness).
CONSISTENCY OF M-VALUES
One observation that can be made about the comparison between the M-values of the various algorithms is that there is not a great difference between them.
In other words, there appears to be a certain consistency between the values determined by various independent researchers around the globe.
This is a good sign as it indicates that the science has determined a relatively consistent threshold for symptoms of decompression sickness across the human population.
FORMAT FOR M-VALUES
M-values are often expressed in the form of a linear equation as in the Workman-style or the Bühlmann-style. This format is ideal for computer programming since it allows the M-values to be calculated “on-the-fly” as they are needed. The linear format permits the display of M-value lines on the pressure graph as well.
M-values can also be expressed in the form of a matrix or table. This is simply where the M-values for each half-time compartment and each stop depth are pre-calculated and arranged in columns and rows.
This format is useful for detailed comparisons and analysis. Some of the early dive computers and desktop computer programs used the table format to “look up” M-values for each stop during the calculation process.
Sponsored Link
M-VALUE CHARACTERISTICS
M-value sets can be classified into two categories, no-decompression sets and decompression sets. No-decompression M-values are surfacing values only. The DSAT RDP M-values are an example.
No-Stop Dive Profiles
No-stop dive profiles are designed so that the calculated gas loadings in the compartments do not exceed the surfacing M-values. This allows for direct ascent to the surface at any time during the dive. Some no-decompression algorithms account for ascent and descent rates in the calculations.
Decompression Profiles
Decompression M-values are characterized by having a slope parameter which determines the change in M-value with change in ambient pressure. The value of the slope parameter will vary depending on the half-time of the hypothetical “tissue” compartment.
Generally, faster half-time compartments will have a greater slope than slower half-time compartments. This reflects the observation that faster compartments tolerate greater overpressure than slower compartments.
If the slope is greater than 1.0 then the M-value line “expands” on the pressure graph and that compartment will tolerate greater overpressure gradients with increasing depth.
A fixed slope of 1.0 means that the compartment will tolerate the same overpressure gradient regardless of depth.
In all cases, the value of the slope can never be less than 1.0.
Otherwise, the M-value line would cross under the ambient pressure line at some point and this would represent an illogical situation whereby the compartment could not tolerate even the ambient pressure.
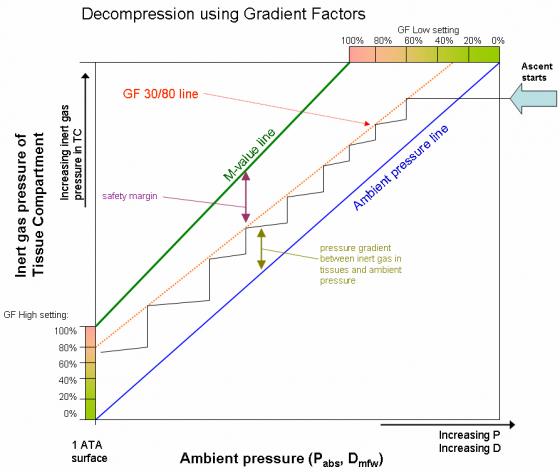
THE AMBIENT PRESSURE LINE
The ambient pressure line is an all-important reference line on the pressure graph. Passing through the origin, it has a slope of 1.0 and simply represents the collection of points where the compartment inert gas loading will be equal to ambient pressure.
This is important because when the inert gas loading in a compartment goes above the ambient pressure line, an overpressure gradient is created.
An M-value line represents the established limit for tolerated overpressure gradient above the ambient pressure line.
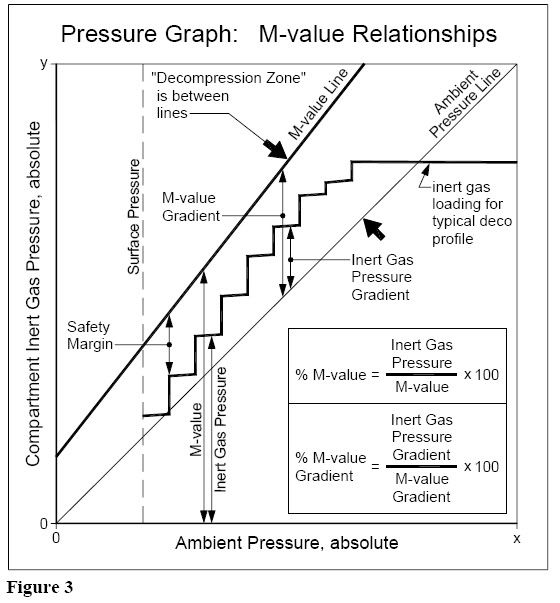
THE DECOMPRESSION ZONE
The “decompression zone” is the region on the pressure graph between the ambient pressure line and the M-value line (see Figure 3).
Within the context of the dissolved gas model, this zone represents the functional area in which decompression should take place.
In theory, a positive gradient above ambient pressure of some magnitude is required in order for a compartment to “off-gas” or “decompress” in an optimum manner.
Depending on the fraction of oxygen in the mix, a compartment may still be able to off-gas even though the total inert gas partial pressure is less than ambient pressure.
However, an “efficient” decompression profile is characterized by leading compartment gas loadings which plot within the decompression zone.
The gas loadings for various half-time compartments will cross into and then out of the decompression zone during the decompression profile depending upon which compartment is “leading” or “controlling” at the time.
Generally, the faster compartments will cross into the decompression zone first and be leading (gas loadings closest to M-value lines) and then the rest of the decompression profile will be controlled by the slower compartments in sequence.
MULTIPLE INERT GASES
Present-day dissolved gas models employ a concept for multiple inert gases which states that the total inert gas pressure in a hypothetical “tissue” compartment is the sum of the partial pressures of the inert gases present in the compartment, even though the various inert gases each have a different half-time for that compartment.
Mixed gas decompression algorithms must deal with more than one inert gas in the breathing mix, such as helium and nitrogen in trimix. M-values for this situation are handled differently by the various algorithms.
Some methodologies use the same M-values for both nitrogen and helium; usually they are based on the M-values for nitrogen.
In the Bühlmann algorithm, an intermediate M-value is calculated which is an adjustment between the separate M-values for nitrogen and helium based on the proportion of these inert gases present in the compartment.
In the M-value linear equation, the Coefficient a (He+N2) and the Coefficient b (He+N2) are computed in accordance with the partial pressures of helium (PHe) and nitrogen (PN2) as follows:
a (He+N2) = [a (He)×PHe + a (N2)×PN2] / [PHe + PN2];
b (He+N2) = [b (He)×PHe + b (N2)×PN2] / [PHe + PN2].
Become A Shearwater Power User! (eBook)
An Illustrated Guide to Gradient Factors and Advanced Shearwater Computer Settings for safe scuba diving.
42 Pages. Printable PDF format. Fully Illustrated.$9
A misconception among some divers is that M-values represent a hard line between “getting the bends” and “not getting the bends.” This might explain why some divers routinely push the limits of their tables or dive computers.
The experience of diving medicine has shown that the established limits (M-values) are sometimes inadequate. The degree of inadequacy is seen to vary with the individual and the situation.
Accordingly, it may be more appropriate to describe an M-value as “a solid line drawn through a fuzzy, gray area” (see Figure 2).
The reasons for this lack of definitude involve complex human physiology, variations among individuals, and predisposing factors for decompression sickness.
Dissolved Gas Models
Overall, the dissolved gas model has worked well for divers and the knowledge base has continued to grow. For example, it was originally presumed that all inert gas had to remain dissolved in solution and that any bubbles were indicative of DCS.
The Existence of Silent Bubbles
However, we now know that silent bubbles are present even during symptom-free dives. Thus, the reality is that there is a combination of two conditions during a dive _ most of the inert gas presumably in solution and some of the inert gas out of solution as bubbles.
An M-value, therefore, represents not only a tolerable overpressure gradient, but a tolerable amount of bubbles as well.
M-values are empirically verified, meaning that actual decompression trials are carried out with human subjects. These tests are conducted with a relatively small number of subjects intended to represent the much larger population of divers.
Even though good data is obtained about the approximate threshold for symptoms of decompression sickness (M-values), this process cannot accurately predict or guarantee an absolute threshold for everyone.
DCS Predisposing Factors
Also, we know from experience that certain factors are predisposing for decompression sickness: lack of physical conditioning, fattiness, fatigue, drugs/alcohol, dehydration, over-exertion, very cold water, open patent foramen ovale (PFO), etc. Individual susceptibility can vary on a daily basis as well.
M-VALUES AND CONSERVATISM
Limited symptoms, if any, and a reasonably low level of risk are associated with M-values. This criteria, however, may not be entirely acceptable to all divers. Many divers would like to be in the range of “no symptoms” and “very low level of risk” when it comes to their decompression profiles.
Fortunately, it is well understood among decompression modelers and programmers that calculations based on the established M-values alone cannot produce sufficiently reliable decompression tables for all individuals and all scenarios.
A Method For Introducing Conservatism
This is why decompression programs provide for a means of introducing conservatism into the calculations.
Some of the methodologies include increasing the inert gas fractions used in the calculations, applying a depth safety factor which calculates for a deeper-than-actual dive depth, calculating for a longer-than-actual bottom time, and adjusting the half-times to be asymmetrical during off-gassing (slower). Some programs use more than one of these methods combined.
These methodologies for conservatism are effective when properly applied. The degree of “effectiveness” is usually gauged by divers in terms of how much longer and deeper the decompression profiles become, and through individual experience with the outcome of the profiles.
M-VALUE RELATIONSHIPS
Some fundamental relationships involving M-values and decompression calculations are indicated on the pressure graph in Figure 3.
The Percent M-value calculation has been used by various decompression modelers over the years. Professor Bühlmann, for example, evaluated many of his decompression trials on a Percent M-value basis and reported the data as such in his book(s).
The Percent M-value Gradient calculation is a measure of how far a decompression profile has entered into the decompression zone.
0% M-value Gradient is at the ambient pressure line and represents the bottom of the decompression zone.
100% M-value Gradient is at the M-value line and represents the top of the decompression zone.
ANALYSIS OF DECOMPRESSION PROFILES
Many divers would like to know precisely what the effect is of the conservatism factors in their desktop decompression program(s). They realize that longer and deeper profiles are generated with increasing conservatism factors, but more fundamental information is desired.
Both the Percent M-value and Percent M-value Gradient relationships are useful for the analysis and evaluation of decompression profiles.
Using a standard set of reference M-values, different profiles can be evaluated on a consistent basis. This includes comparison of profiles generated by entirely different programs, algorithms, and decompression models.
UNIVERSAL REFERENCE VALUES
The Bühlmann ZH-L16 M-values are employed in most, if not all, of the desktop decompression programs in use by technical divers.
These M-values were developed and tested for a broad range of ambient pressure exposures; from high altitude diving to deep sea diving. When used with appropriate conservatism, they have proven to be “reliable” for technical diving (to the extent that something can be reliable in an inexact science).
They have become the de facto world-wide standard that can serve as universal reference values for the comparison and evaluation of decompression profiles.
It is a relatively easy task for programmers to include Percent M-value and Percent M-value Gradient calculations in summary form with the decompression profiles.
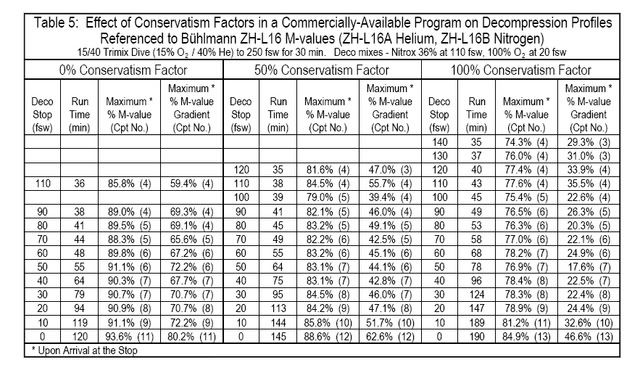
Table 5 is an example of this and shows the effect of conservatism factors used in a commercially-available desktop decompression program. At 0% Conservatism Factor, the decompression profile is in the 90% M-value range and has entered approximately 70% into the decompression zone (70% M-value Gradient).
It is evident that this program employs a level of baseline conservatism since none of the values reaches 100%. At 50% Conservatism Factor (which is recommended in the user’s manual), the profile is in the 85% M-value range and has entered approximately 40-50% into the decompression zone.
At 100% Conservatism Factor, the profile is in the 77% M-value range and has entered approximately 20-35% into the decompression zone.
Note that the values given in Table 5 are upon arrival the respective stops which is the worst-case condition. This correlates with the edges of the “stair-steps” in the gas loading profile on the pressure graph (see example in Figure 3).
The highest values across all profiles are calculated upon arrival at the surface which illustrates why a very slow final ascent from the last decompression stop to the surface is always prudent.
MARGIN OF SAFETY
Using the M-value relationships and a standard set of reference M-values, divers can determine personal decompression limits which are both well-defined and transportable.
The margin of safety selected will depend on individual disposition and prior experience with profiles. An honest assessment of one’s fitness for decompression diving is always in order.
For example, this author/diver (an office worker) has chosen a personal limit of 85% M-value and 50-60% M-value Gradient for typical trimix dives.
To ensure a fixed margin of safety, a decompression profile can be calculated directly to a predetermined percentage of the M-value Gradient.
The advantage of this approach is complete consistency across the entire ambient pressure range and precise control over the resultant profile.
About the Author: Erik C. Baker
Erik C. Baker is an electrical engineer with an architecture/engineering firm in Pennsylvania. He pursues research into decompression and diving physiology as a hobby, and has developed several FORTRAN computer programs for decompression calculation and analysis. Erik is a certified cave diver and trimix diver.
Decompression References:
Bennett PB, Elliott DH, eds. 1993. The physiology and medicine of diving. London: WB Saunders.
Boycott AE, Damant GCC, Haldane JS. 1908. The prevention of compressed air illness. J Hyg (London) 8:342-443.
Hamilton RW, Muren A, Röckert H, Örnhagen H. 1988. Proposed new Swedish air decompression tables. In: Shields TG, ed. XIVth Annual Meeting of the EUBS. European Undersea Biomedical Society. Aberdeen: National Hyperbaric Center.
Hamilton RW, Rogers RE, Powell MR, Vann RD. 1994. Development and validation of no-stop decompression procedures for recreational diving: The DSAT Recreational Dive Planner. Santa Ana, CA: Diving Science and Technology Corp.
Schreiner HR, Kelley PL. 1971. A pragmatic view of decompression. In: Lambertsen CJ, ed. Underwater Physiology IV. New York: Academic Press.
Wienke BR. 1991. Basic decompression theory and application. Flagstaff, AZ: Best Publishing Co.
Wienke BR. 1994. Basic diving physics and applications. Flagstaff, AZ: Best Publishing Co.
Workman RD. 1965. Calculation of decompression schedules for nitrogen-oxygen and helium-oxygen dives. Research Report 6-65. Washington: Navy Experimental Diving Unit.
Workman RD. 1969. American decompression theory and practice. In: Bennett PB, Elliott DH, eds. The physiology and medicine of diving and compressed air work. London: Baillière, Tindall & Cassell.
Become A Shearwater Power User! (eBook)
An Illustrated Guide to Gradient Factors and Advanced Shearwater Computer Settings for safe scuba diving.
42 Pages. Printable PDF format. Fully Illustrated.$9
Gradient Factors Explained By Matti Antilla Ph.d Gradient Factors Explained I have reproduced this excellent article Gradient Factors explained by Matti Anttila in case the original website goes down. It is published…
Technical Diving Standard Gas Mixes The technical diving standard gas mixes. These breathing gasses ensure risk mitigation and help standardize team tech diving.
Calculating No Stop Time for Scuba Diving Calculating No Stop Time for Scuba Diving Welcome to an informative article on "Calculating No Stop Time for Scuba Diving" written by Erik C. Baker.…
Oxygen Toxicity Dangers by Dr. E.D. Thalmann | DAN DAN discusses the dangers of oxygen toxicity when using nitrox as a breathing gas. By Dr. E.D. Thalmann, DAN Assistant Medical Director; Captain, Medical Corps,…
Gradient Factors for Dummies Gradient Factors for Dummies by Kevin Watts An explanation of gradient factors settings on your deco software.
Hyperbaric Oxygen Therapy (HBOT) What is Hyperbaric Oxygen Therapy (HBOT)? ANDI International Hyperbaric Research Center 74 Woodcleft Ave, Freeport NY 11520 516-546-2026 Article reproduced courtesy of Bruce Konefe Hyperbaric…
Decompression Theory Resources | Technical Scuba Diving Decompression Theory - Links and Resources Here is my selection of educational articles and resources for further reading on scuba diving decompression theory... - Bubble Decompression…
In conjunction with an array of hypothetical “tissue” compartments, gas loading calculations and M-values compose the major elements of the dissolved gas or “Haldanian” decompression model.
